Lets Write a Compiler!

Our goal is to write a compiler which is a function:

compiler :: SourceProgram -> TargetProgram

In 131 TargetProgram is going to be a binary executable.

Lets write our first Compilers

SourceProgram will be a sequence of four tiny “languages”

1. Numbers

• e.g. 7, 12, 42 …

2. Numbers + Increment

• e.g. add1(7), add1(add1(12)), …

3. Numbers + Increment + Decrement

• e.g. add1(7), add1(add1(12)), sub1(add1(42))

4. Numbers + Increment + Decrement + Local Variables

• e.g. let x = add1(7), y = add1(x) in add1(y)

Recall: What does a Compiler look like?

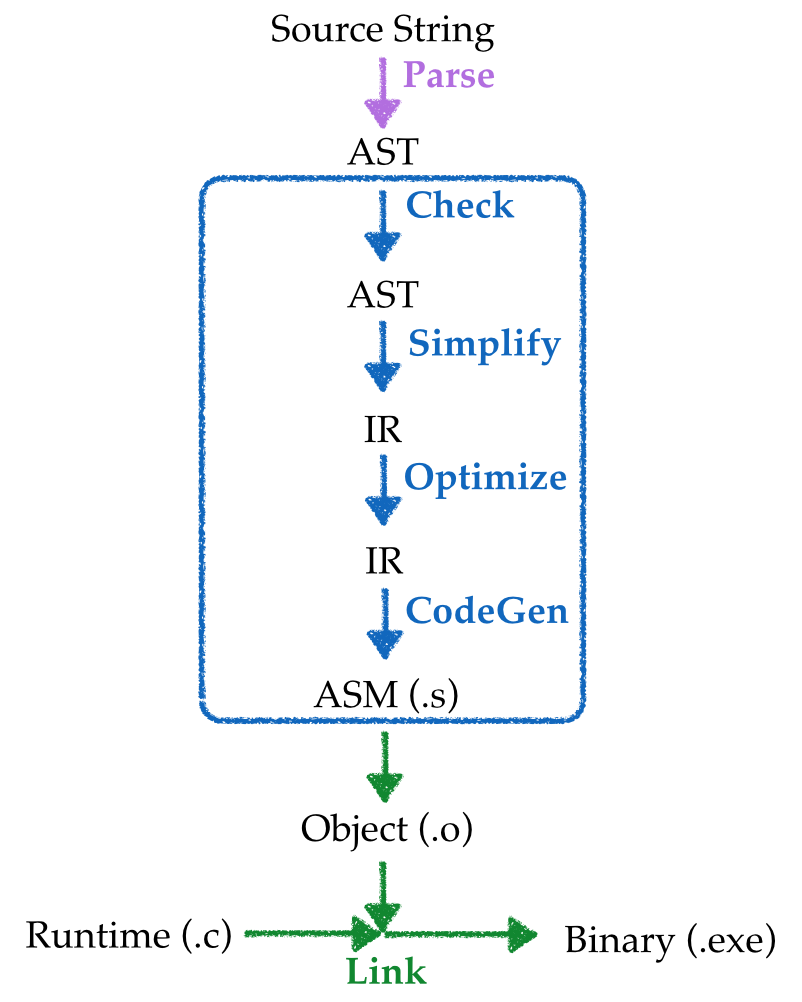
An input source program is converted to an executable binary in many stages:

• Parsed into a data structure called an Abstract Syntax Tree
• Checked to make sure code is well-formed (and well-typed)
• Simplified into some convenient Intermediate Representation
• Optimized into (equivalent) but faster program
• Generated into assembly x86
• Linked against a run-time (usually written in C)

Simplified Pipeline

Goal: Compile source into executable that, when run, prints the result of evaluating the source.

Approach: Lets figure out how to write

1. A compiler from the input string into assembly,
2. A run-time that will let us do the printing.

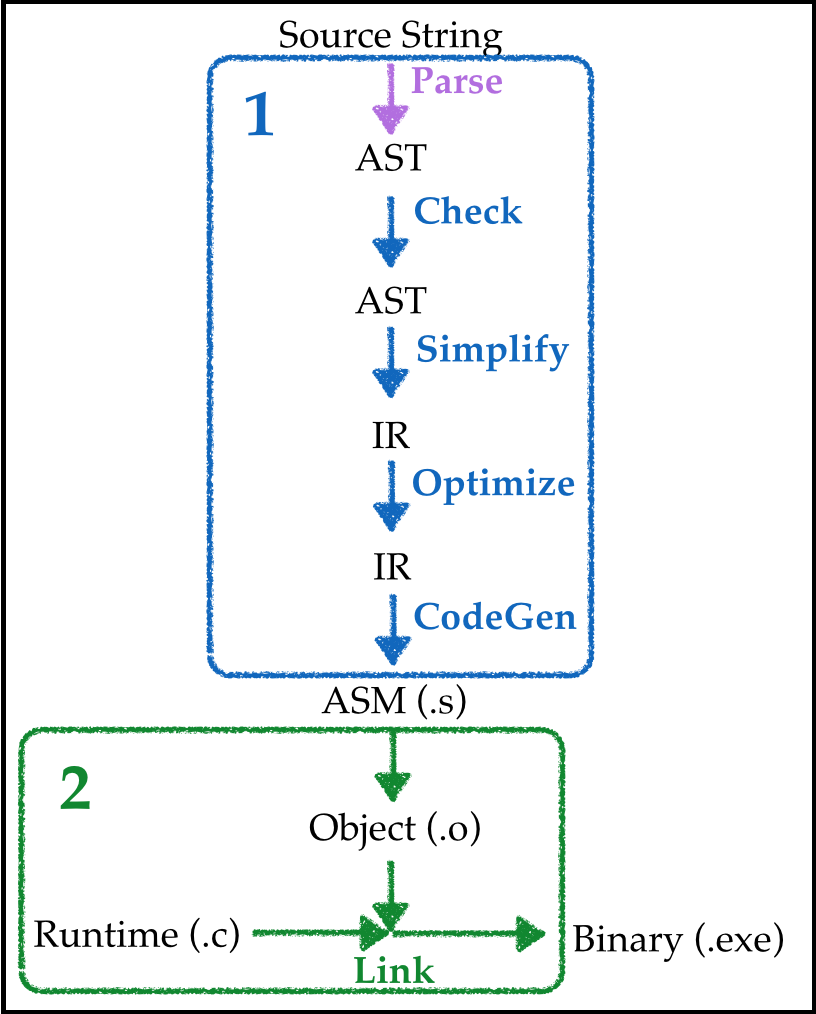
Next, lets see how to do (1) and (2) using our sequence of adder languages.

Adder-1

1. Numbers

• e.g. 7, 12, 42 …

The “Run-time”

Lets work backwards and start with the run-time.

Here’s what it looks like as a C program main.c

#include <stdio.h>

extern int our_code() asm("our_code_label");

int main(int argc, char** argv) {
  int result = our_code();
  printf("%d\n", result);
  return 0;
}

main just calls our_code and prints its return value

our_code is (to be) implemented in assembly,

• Starting at label our_code_label,

• With the desired return value stored in register RAX

• per, the C calling convention

Test Systems in Isolation

Key idea in (Software) Engineering:

Decouple systems so you can test one component without (even implementing) another.

Lets test our “run-time” without even building the compiler.

Testing the Runtime: A Really Simple Example

Given a SourceProgram

42

We want to compile the above into an assembly file forty_two.s that looks like:

section .text
global our_code_label
our_code_label:
  mov rax, 42
  ret

For now, lets just

• write that file by hand, and test to ensure
• object-generation and then
• linking works

(On MacOS)

$ nasm -f macho64 -o forty_two.o forty_two.s
$ clang -g -m64 -o forty_two.run c-bits/main.c forty_two.o

(On Linux)

$ nasm -f elf64 -o forty_two.o forty_two.s
$ clang -g -m64 -o forty_two.run c-bits/main.c forty_two.o

We can now run it:

$ forty_two.run
42

Hooray!

The “Compiler”

Recall, that compilers were invented to avoid writing assembly by hand

First Step: Types

To go from source to assembly, we must do:

Our first step will be to model the problem domain using types.

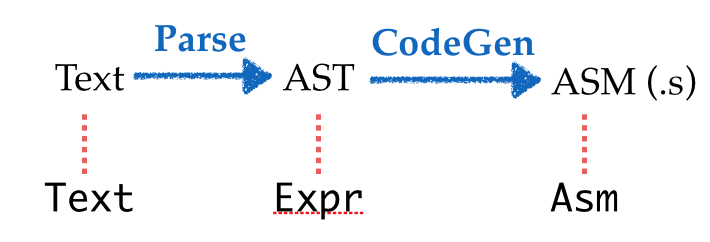
Lets create types that represent each intermediate value:

• Text for the raw input source
• Expr for the AST
• Asm for the output x86 assembly

Defining the Types: Text

Text is raw strings, i.e. sequences of characters

texts :: [Text]
texts =
  [ "It was a dark and stormy night..."
  , "I wanna hold your hand..."
  , "12"
  ]

Defining the Types: Expr

We convert the Text into a tree-structure defined by the datatype

data Expr = Number Int

Note: As we add features to our language, we will keep adding cases to Expr.

Defining the Types: Asm

Lets also do this gradually as the x86 instruction set is HUGE!

Recall, we need to represent

section .text
global our_code_label
our_code_label:
  mov rax, 42
  ret

An Asm program is a list of instructions each of which can:

• Create a Label, or
• Move a Arg into a Register
• Return back to the run-time.

type Asm = [Instruction]

data Instruction
  = ILabel Text
  | IMov   Arg Arg
  | IRet

Where we have

data Register
  = RAX

data Arg
  = Const Int       -- a fixed number
  | Reg   Register  -- a register

Second Step: Transforms

Ok, now we just need to write the functions:

parse   :: Text -> Expr     -- 1. Transform source-string into AST
compile :: Expr -> Asm      -- 2. Transform AST into assembly
asm     :: Asm  -> Text     -- 3. Transform assembly into output-string

Pretty straightforward:

parse :: Text -> Expr
parse    = parseWith expr
  where
    expr = integer

compile :: Expr -> Asm
compile (Number n) =
  [ IMov (Reg RAX) (Const n)
  , IRet
  ]

asm :: Asm -> Text
asm is = L.intercalate "\n" [instr i | i <- is]

Where instr is a Text representation of each Instruction

instr :: Instruction -> Text
instr (IMov a1 a2) = printf "mov %s, %s" (arg a1) (arg a2)

arg :: Arg -> Text
arg (Const n) = printf "%d" n
arg (Reg r)   = reg r

reg :: Register -> Text
reg RAX = "rax"

Brief digression: Type-Classes

Note that above we have four separate functions that crunch different types to the Text representation of x86 assembly:

asm   :: Asm -> Text
instr :: Instruction -> Text
arg   :: Arg -> Text
reg   :: Register -> Text

Remembering names is hard.

We can write an overloaded function, and let the compiler figure out the correct implementation from the type, using Type-Classes.

The following defines an interface for all those types a that can be converted to x86 assembly:

class ToX86 a where
  asm :: a -> Text

Now, to overload, we say that each of the types Asm, Instruction, Arg and Register implements or has an instance of ToX86

instance ToX86 Asm where
  asm is = L.intercalate "\n" [asm i | i <- is]

instance ToX86 Instruction where
  asm (IMov a1 a2) = printf "mov %s, %s" (asm a1) (asm a2)

instance ToX86 Arg where
  asm (Const n) = printf "%d" n
  asm (Reg r)   = asm r

instance ToX86 Register where
  asm RAX = "rax"

Note in each case above, the compiler figures out the correct implementation, from the types…

Adder-2

Well that was easy! Lets beef up the language!

2. Numbers + Increment

• e.g. add1(7), add1(add1(12)), …

Repeat our Recipe

1. Build intuition with examples,
2. Model problem with types,
3. Implement compiler via type-transforming-functions,
4. Validate compiler via tests.

1. Examples

First, lets look at some examples.

Example 1

How should we compile?

add1(7)

In English

1. Move 7 into the rax register
2. Add 1 to the contents of rax

In ASM

mov rax, 7
add rax, 1

Aha, note that add is a new kind of Instruction

Example 2

How should we compile

add1(add1(12))

In English

1. Move 12 into the rax register
2. Add 1 to the contents of rax
3. Add 1 to the contents of rax

In ASM

mov rax, 12
add rax, 1
add rax, 1

Compositional Code Generation

Note correspondence between sub-expressions of source and assembly

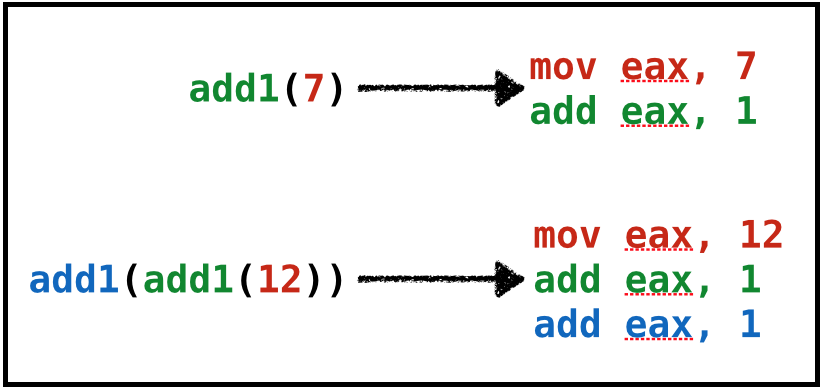
We will write compiler in compositional manner

• Generating Asm for each sub-expression (AST subtree) independently,
• Generating Asm for super-expression, assuming the value of sub-expression is in RAX

2. Types

Next, lets extend the types to incorporate new language features

Extend Type for Source and Assembly

Source Expressions

data Expr = ...
          | Add1   Expr

Assembly Instructions

data Instruction
  = ...
  | IAdd  Arg Arg

Example-1 Revisited

src1 = "add1(7)"

exp1 = Add1 (Number 7)

asm1 = [ IMov (Reg RAX) (Const 7)
       , IAdd (Reg RAX) (Const 1)
       ]

Example-2 Revisited

src2 = "add1(add1(12))"

exp2 = Add1 (Add1 (Number 12))

asm2 = [ IMov (Reg RAX) (Const 12)
       , IAdd (Reg RAX) (Const 1)
       , IAdd (Reg RAX) (Const 1)
       ]

3. Transforms

Now lets go back and suitably extend the transforms:

parse   :: Text -> Expr     -- 1. Transform source-string into AST
compile :: Expr -> Asm      -- 2. Transform AST into assembly
asm     :: Asm  -> Text     -- 3. Transform assembly into output-string

Lets do the easy bits first, namely parse and asm

Parse

parse :: Text -> Expr
parse = parseWith expr

expr :: Parser Expr
expr =  try primExpr
    <|> integer

primExpr :: Parser Expr
primExpr = Add1 <$> rWord "add1" *> parens expr

Asm

To update asm just need to handle case for IAdd

instance ToX86 Instruction where
  asm (IMov a1 a2) = printf "mov %s, %s" (asm a1) (asm a2)
  asm (IAdd a1 a2) = printf "add %s, %s" (asm a1) (asm a2)

Note

1. GHC will tell you exactly which functions need to be extended (Types, FTW!)
2. We will not discuss parse and asm any more…

Compile

Finally, the key step is

compile :: Expr -> Asm
compile (Number n)
  = [ IMov (Reg RAX) (Const n)
    ]

compile (Add1 e)
  = compile e                    -- RAX holds value of result of `e` ...
 ++ [ IAdd (Reg RAX) (Const 1) ] -- ... so just increment it.

Examples Revisited

Lets check that compile behaves as desired:

>>> (compile (Number 12)
[ IMov (Reg RAX) (Const 12) ]

>>> compile (Add1 (Number 12))
[ IMov (Reg RAX) (Const 12)
, IAdd (Reg RAX) (Const 1)
]

>>> compile (Add1 (Add1 (Number 12)))
[ IMov (Reg RAX) (Const 12)
, IAdd (Reg RAX) (Const 1)
, IAdd (Reg RAX) (Const 1)
]

Adder-3

You do it!

3. Numbers + Increment + Double

• e.g. add1(7), twice(add1(12)), twice(twice(add1(42)))

Adder-4

4. Numbers + Increment + Decrement + Local Variables

• e.g. let x = add1(7), y = add1(x) in add1(y)

Can you think why local variables make things more interesting?

Repeat our Recipe

1. Build intuition with examples,
2. Model problem with types,
3. Implement compiler via type-transforming-functions,
4. Validate compiler via tests.

Step 1: Examples

Lets look at some examples

Example: let1

let x = 10
in
    x

Need to store 1 variable – x

Example: let2

let x = 10         -- x = 10
  , y = add1(x)    -- y = 11
  , z = add1(y)    -- z = 12
in
    add1(z)        -- 13

Need to store 3 variables– x, y, z

Example: let3

let a = 10
  , c = let b = add1(a)
        in
           add1(b)
in
    add1(c)

Need to store 3 variables – a, b, c – but at most 2 at a time

• First a, b, then a, c
• Don’t need b and c simultaneously

Problem: Registers are Not Enough

A single register rax is useless:

• May need 2 or 3 or 4 or 5 … values.

There is only a fixed number (say, N) of registers

• And our programs may need to store more than N values, so

Need to dig for more storage space!

Memory: Code, Globals, Heap and Stack

Here’s what the memory – i.e. storage – looks like:

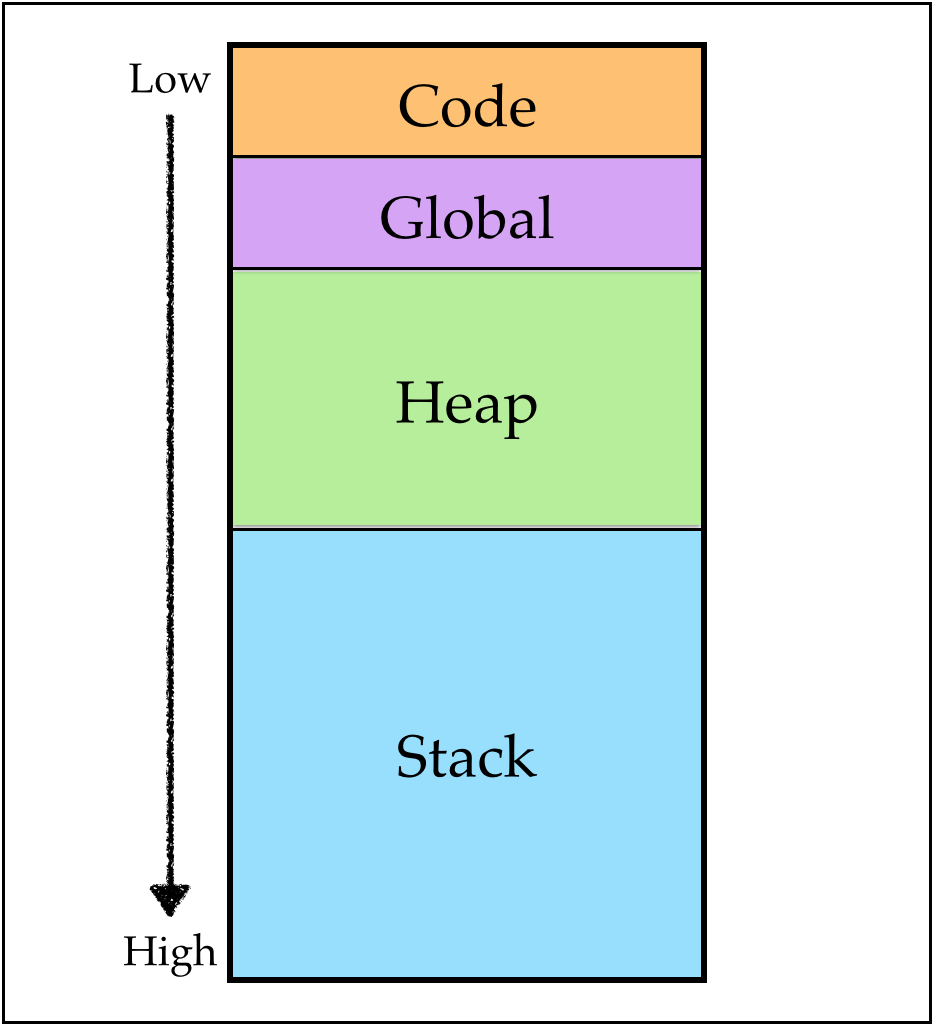
Focusing on “The Stack”

Lets zoom into the stack region, which when we start looks like this:

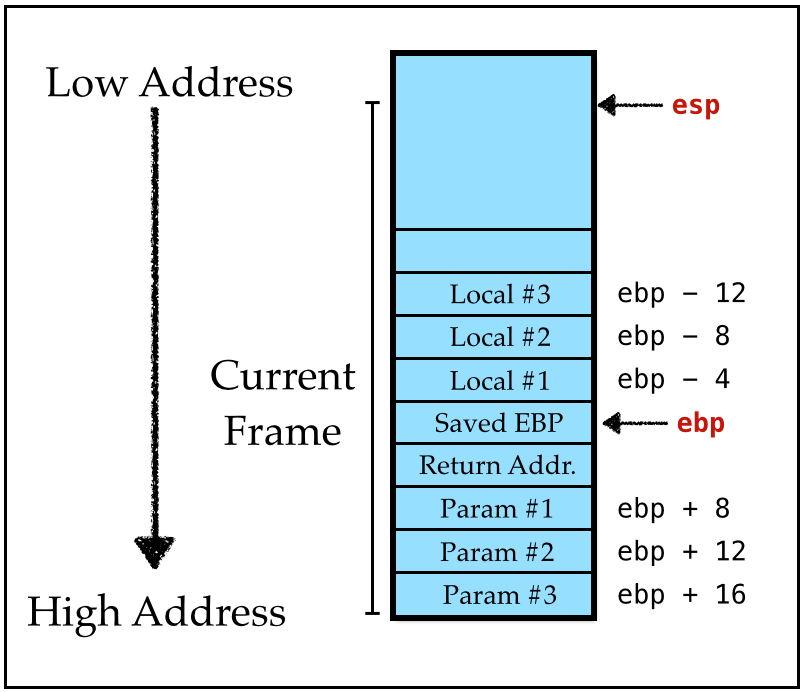
The stack grows downward (i.e. to smaller addresses)

We have lots of 8-byte slots on the stack at offsets from the “stack pointer” at addresses:

• [RBP - 8 * 1], [RBP - 8 * 2], [RBP - 8 * 3] …,

Note: On 32-bit machines

• We’d use the rax register (vs rax in 64-bit)
• The “base” is the ebp register (vs rbp in 64-bit)
• Each slot is 4-bytes (vs 8 in 64-bit)

How to compute mapping from variables to slots ?

The i-th stack-variable lives at address [RBP - 8 * i]

Required A mapping

• From source variables (x, y, z …)
• To stack positions (1, 2, 3 …)

Solution The structure of the lets is stack-like too…

• Maintain an Env that maps Id |-> StackPosition

let x = e1 in e2 adds x |-> i to Env

• where i is ``current’’ size of stack.

Let-bindings and Stacks: Example-1

                    -- []
let x = 1
in                  -- [ x |-> 1 ]
    x

Let-bindings and Stacks: Example-2

                          -- []
let x = 1
                          -- [x |-> 1]
  , y = add1(x)
                          -- [y |-> 2, x |-> 1]
  , z = add1(y)
in                        -- [z |- 3, y |-> 2, x |-> 1]
    add1(z)

QUIZ

At what position on the stack do we store variable c ?

let a = 1
  , c =
        let b = add1(a)
        in add1(b)
in
    add1(c)

A. 1

B. 2

C. 3

D. 4

E. not on stack!

Strategy

              -- ENV(n)
let x = E1
in            -- [x |-> n+1, ENV(n)]
   E2
              -- ENV(n)

Strategy: Variable Definition

At each point, we have env that maps (previously defined) Id to StackPosition

To compile let x = e1 in e2 we

1. Compile e1 using env (i.e. resulting value will be stored in rax)
2. Move rax into [RBP - 8 * i]
3. Compile e2 using env'

(where env' be env with x |-> i i.e. push x onto env at position i)

Strategy: Variable Use

To compile x given env

1. Move [RBP - 8 * i] into rax

(where env maps x |-> i)

Example: Let-bindings to Asm

Lets see how our strategy works by example:

Example: let1

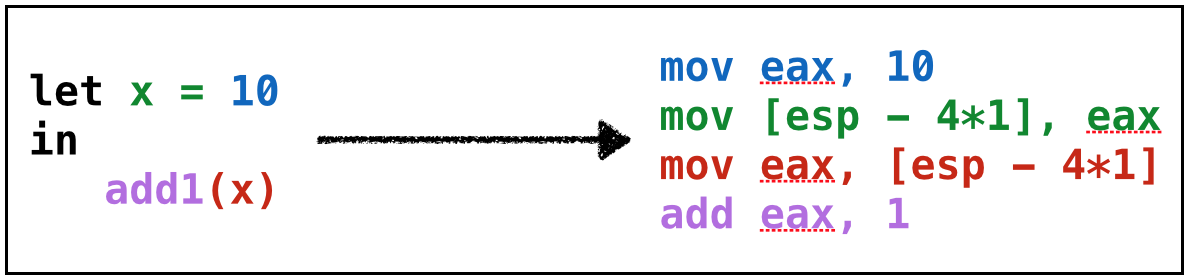
QUIZ: let2

When we compile

let x = 10
  , y = add1(x)
in
  add1(y)

The assembly looks like

mov rax, 10                ; LHS of let x = 10
mov [RBP - 8*1], rax       ; save x on the stack
mov rax, [RBP - 8*1]       ; LHS of   , y = add1(x)
add rax, 1                 ; ""
???
add rax, 1

What .asm instructions shall we fill in for ???

mov [RBP - 8 * 1], rax    ; A
mov rax, [RBP - 8 * 1]

mov [RBP - 8 * 1], rax    ; B

mov [RBP - 8 * 2], rax    ; C

mov [RBP - 8 * 2], rax    ; D
mov rax, [RBP - 8 * 2]

                          ; E  (empty! no instructions)

Example: let3

Lets compile

let a = 10
  , c = let b = add1(a)
        in
            add1(b)
in
    add1(c)

Lets figure out what the assembly looks like!

mov rax, 10                ; LHS of let a = 10
mov [RBP - 8*1], rax       ; save a on the stack
???

Step 2: Types

Now, we’re ready to move to the implementation!

Source Expressions

type Id   = Text

data Expr = ...
          | Let Id Expr Expr    -- `let x = e1 in e2` represented as `Let x e1 e2`
          | Var Id              -- `x` represented as `Var x`

Assembly Instructions

Lets enrich the Instruction to include the register-offset [RBP - 8*i]

data Arg = ...
         | RegOffset Reg Int    -- `[RBP - 8*i]` modeled as `RegOffset RBP i`

Environments

An Env type to track stack-positions of variables with API

• push variable onto Env (returning its position),
• lookup a variable’s position in Env

push :: Id -> Env -> (Int, Env)
push x env = (i, (x, i) : env)
  where
    i      = 1 + length env

lookup :: Id -> Env -> Maybe Int
lookup x ((y, i) : env)
  | x == y              = Just i
  | otherwise           = lookup x env
lookup x []             = Nothing

Step 3: Transforms

Almost done: just write code formalizing the above strategy

Code: Variable Use

compileEnv env (Var x) = [ IMov (Reg RAX) (RegOffset RBP i) ]
  where
    i                  = fromMaybe err (lookup x env)
    err                = error (printf "Error: Variable '%s' is unbound" x)

Code: Variable Definition

compileEnv env (Let x e1 e2 l)  = compileEnv env  e1
                               ++ IMov (RegOffset RBP i) (Reg RAX)
                                : compileEnv env' e2
      where
        (i, env')               = pushEnv x env

Step 4: Tests

Lets take our adder compiler out for a spin!

Recap: We just wrote our first Compilers

SourceProgram will be a sequence of four tiny “languages”

1. Numbers

• e.g. 7, 12, 42 …

2. Numbers + Increment

• e.g. add1(7), add1(add1(12)), …

3. Numbers + Increment + Decrement

• e.g. add1(7), add1(add1(12)), sub1(add1(42))

4. Numbers + Increment + Decrement + Local Variables

• e.g. let x = add1(7), y = add1(x) in add1(y)

Using a Recipe

1. Build intuition with examples,
2. Model problem with types,
3. Implement compiler via type-transforming-functions,
4. Validate compiler via tests.

Will iterate on this till we have a pretty kick-ass language.