Next, lets add support for
- Multiple datatypes (
numberandboolean) - Calling external functions
In the process of doing so, we will learn about
- Tagged Representations
- Calling Conventions
Plan
Our plan will be to (start with boa) and add the following features:
Representing boolean values (and numbers)
Arithmetic Operations
Arithmetic Comparisons
Dynamic Checking (to ensure operators are well behaved)
1. Representation
Motivation: Why booleans?
In the year 2021, its a bit silly to use
0forfalseand- non-zero for
true.
But really, boolean is a stepping stone to other data
- Pointers
- Tuples
- Structures
- Closures
The Key Issue
How to distinguish numbers from booleans?
- Need extra information to mark values as
numberorbool.
A Word
(A reminder for me, since I always get mixed up)
- A Bit is 1-bit
- A Byte is 8-bits
- A Word is 2-bytes = 16 bits
- A Double Word is 2-words = 4-bytes = 32 bits
- A Quad Word is 4-words = 8-bytes = 64 bits
We are working in x86_64 where the default size is a qword
- Registers are 64-bits
- Arithmetic is 64-bits
- Stack slots should be 64-bits
- etc.
Option 1: Use Two (Quad-)Words
How to distinguish numbers from booleans?
Need extra information to mark values as
numberorbool.
First word is 0 means bool, is 1 means number, 2 means pointer etc.
| Value | Representation (HEX) |
|---|---|
3 |
[0x000000000][0x00000003] |
5 |
[0x000000000][0x00000005] |
12 |
[0x000000000][0x0000000c] |
42 |
[0x000000000][0x0000002a] |
false |
[0x000000001][0x00000000] |
true |
[0x000000001][0x00000001] |
Pros
- Can have lots of different types, but
Cons
Takes up double memory,
Operators
+,-require two memory reads.
In short, rather wasteful! We don’t need so many types.
Option 2: Use a Tag Bit
Can distinguish two types with a single bit.
Least Significant Bit (LSB) is
0fornumber1forboolean
Question: why not 0 for boolean and 1 for number?
Tag Bit: Numbers
So number is the binary representation shifted left by 1 bit
- Lowest bit is always
0 - Remaining bits are number’s binary representation
For example, in binary:
| Value | Representation (Binary) |
|---|---|
3 |
[0b00000110] |
5 |
[0b00001010] |
12 |
[0b00011000] |
42 |
[0b01010100] |
Or in hexadecimal:
| Value | Representation (HEX) |
|---|---|
3 |
[0x06] |
5 |
[0x0a] |
12 |
[0x18] |
42 |
[0x54] |
Tag Bit: Booleans
Most Significant Bit (MSB) is
1fortrue0forfalse
For example
| Value | Representation (Binary) |
|---|---|
true |
[0b10000000000000000000000000000001] |
false |
[0b00000000000000000000000000000001] |
Or, in HEX
| Value | Representation (HEX) |
|---|---|
true |
[0x80000001] |
false |
[0x00000001] |
(eliding the 32/8 zeros in the “most-significant” DWORD)
Types
Lets extend our source types with boolean constants
data Expr a
= ...
| Boolean Bool aCorrespondingly, we extend our assembly Arg (values) with
data Arg
= ...
| HexConst IntSo, our examples become:
| Value | Representation (HEX) |
|---|---|
Boolean False |
HexConst 0x00000001 |
Boolean True |
HexConst 0x80000001 |
Number 3 |
HexConst 0x00000006 |
Number 5 |
HexConst 0x0000000a |
Number 12 |
HexConst 0x0000000c |
Number 42 |
HexConst 0x0000002a |
Transforms
Next, lets update our implementation
The parse, anf and tag stages are straightforward.

Lets focus on the compile function.
A TypeClass for Representing Constants
Its convenient to introduce a type class describing Haskell types that can be represented as x86 arguments:
class Repr a where
repr :: a -> ArgWe can now define instances for Int and Bool as:
instance Repr Int where
repr n = Const (Data.Bits.shift n 1) -- left-shift `n` by 1
instance Repr Bool where
repr False = HexConst 0x00000001
repr True = HexConst 0x80000001
Immediate Values to Arguments
Boolean b is an immediate value (like Number n).
Lets extend immArg that transforms an immediate expression to an x86 argument.
immArg :: Env -> ImmTag -> Arg
immArg (Var x _) = ...
immArg (Number n _) = repr n
immArg (Boolean b _) = repr b
Compiling Constants
Finally, we can easily update the compile function as:
compileEnv :: Env -> AnfTagE -> Asm
compileEnv _ e@(Number _ _) = [IMov (Reg RAX) (immArg env e)]
compileEnv _ e@(Boolean _ _) = [IMov (Reg RAX) (immArg env e)](The other cases remain unchanged.)
Lets run some tests to double check.
QUIZ
What is the result of:
ghci> exec "15"A. Error
B. 0
C. 15
D. 30
Output Representation
Say what?! Need to update our run-time printer in main.c
void print(int val){
if (val == CONST_TRUE)
printf("true");
else if (val == CONST_FALSE)
printf("false");
else // should be a number!
printf("%d", d >> 1); // shift right to remove tag bit.
}and now we get:
ghci> exec "15"
15Can you think of some other tests we should write?
QUIZ
What is the result of
ghci> exec "let x = 15 in x"A. Error
B. 0
C. 15
D. 30
QUIZ
What is the result of
>>> exec "if 3: 12 else: 49">>> exec "if 0: 12 else: 49">>> exec "if true: 12 else: 49">>> exec "if false: 12 else: 49"A. Error
B. 0
C. 12
D. 49
Lets go and fix the code so the above do the right thing!
2. Arithmetic Operations
Constants like 2, 29, false are only useful if we can perform computations with them.
First lets see what happens with our arithmetic operators.
QUIZ: Addition
What will be the result of:
ghci> exec "12 + 4"A. Does not compile
B. Run-time error (e.g. segmentation fault)
C. 16
D. 32
E. 0
Shifted Representation and Addition
We are representing a number n by shifting it left by 1
nhas the machine representation2*n
Thus, our source values have the following _representations:
| Source Value | Representation (DEC) |
|---|---|
3 |
6 |
5 |
10 |
3 + 5 = 8 |
6 + 10 = 16 |
n1 + n2 |
2*n1 + 2*n2 = 2*(n1 + n2) |
That is, addition (and similarly, subtraction) works as is with the shifted representation.
QUIZ: Multiplication
What will be the result (using our code so far) of:
ghci> exec "12 * 4"A. Does not compile
B. Run-time error (e.g. segmentation fault)
C. 24
D. 48
E. 96
Shifted Representation and Multiplication
We are representing a number n by shifting it left by 1
nhas the machine representation2*n
Thus, our source values have the following _representations:
| Source Value | Representation (DEC) |
|---|---|
3 |
6 |
5 |
10 |
3 * 5 = 15 |
6 * 10 = 60 |
n1 * n2 |
2*n1 * 2*n2 = 4*(n1 + n2) |
Thus, multiplication ends up accumulating the factor of 2.
- Result is two times the desired one.
Strategy
Thus, our strategy for compiling arithmetic operations is:
Addition and Subtraction “just work” - as shifting “cancels out”,
Multiplication result must be “adjusted” by dividing-by-two
- i.e. right shifting by 1
Types
The source language does not change at all, for the Asm lets add a “right shift” instruction (shr):
data Instruction
= ...
| IShr Arg ArgTransforms
We need only modify compileEnv to account for the “fixing up”
compileEnv :: Env -> AnfTagE -> [Instruction]
compileEnv env (Prim2 o v1 v2 _) = compilePrim2 env o v1 v2where the helper compilePrim2 works for Prim2 (binary) operators and immediate arguments:
compilePrim2 :: Env -> Prim2 -> ImmE -> ImmE -> [Instruction]
compilePrim2 env Plus v1 v2 = [ IMov (Reg RAX) (immArg env v1)
, IAdd (Reg RAX) (immArg env v2)
]
compilePrim2 env Minus v1 v2 = [ IMov (Reg RAX) (immArg env v1)
, ISub (Reg RAX) (immArg env v2)
]
compilePrim2 env Times v1 v2 = [ IMov (Reg RAX) (immArg env v1)
, IMul (Reg RAX) (immArg env v2)
, IShr (Reg RAX) (Const 1)
]Tests
Lets take it out for a drive.
ghci> exec' "2 * (0 - 1)"
4611686018427387902Whoa?!
Well, its easy to figure out if you look at the generated assembly:
mov rax, 4
imul rax, -2
shr rax, 1
ret
Two’s Complement
The negative result is in twos-complement format.
When we shift that right-by-one, we get the odd value
- does not “divide by two”
| Decimal | Hexadecimal |
|---|---|
-8 |
0xFFFFFFFFFFFFFFF8 |
2147483644 |
0x7FFFFFFFFFFFFFFC |
Solution: Signed/Arithmetic Shift
The instruction sar shift arithmetic right does what we want, namely:
- preserves the sign-bit when shifting
- i.e. doesn’t introduce a
0by default
Transforms Revisited
Lets add sar to our target:
data Instruction
= ...
| ISar Arg Argand use it to fix the post-multiplication adjustment
- i.e. use
ISarinstead ofIShr
compilePrim2 env Times v1 v2 = [ IMov (Reg RAX) (immArg env v1)
, IMul (Reg RAX) (immArg env v2)
, ISar (Reg RAX) (Const 1)
]After which all is well:
ghci> exec' "2 * (-1)"
-2
3. Arithmetic Comparisons
Next, lets try to implement comparisons:
ghci> exec "1 < 2"
...
boa: lib/Language/Boa/Compiler.hs:(104,1)-(106,43): Non-exhaustive patterns in function compilePrim2Oops. Need to implement it first!
How to implement comparisons?
Many ways to do this:
branches
jne, jl, jgorbit-twiddling.
Option 1: Comparisons via Branches
Key Idea:
Use the machine comparisons and branch
To implement arg1 < arg2
IF
arg1 < arg2
THEN
rax := <true>
ELSE
rax := <false>
mov rax, <arg1>
cmp rax, <arg2> # flags are set with comparison
jg false_label # if cmp-greater then false else true
mov rax, <true> # assign to RAX := true
jmp exit_label
false_label:
mov rax, <false> # assign to RAX := false
exit_label:
Option 2: Comparisons via Bit-Twiddling
Key idea:
A negative number’s most significant bit is
1
To implement arg1 < arg2, compute arg1 - arg2
- When result is negative, MSB is
1, ensureraxset to0x80000001 - When result is non-negative, MSB is
0, ensureraxset to0x00000001
- Can extract msb by bitwise
andwith0x8000000000000000. - Can shift msb to 32-position with
shr - Can set tag bit by bitwise
orwith0x00000001
So compilation strategy is:
mov rax, arg1
sub rax, arg2
and rax, 0x8000000000000000 ; mask out "sign" bit (msb)
shr rax, 32 ; shift "sign" bit (msb) by 32
or rax, 0x00000001 ; set tag bit to bool
Comparisons: Implementation
Lets go and extend:
- The
Instructiontype
data Instruction
= ...
| IAnd Arg Arg
| IOr Arg Arg- The
instrAsmconverter
instrAsm :: Instruction -> Text
instrAsm (IAnd a1 a2) = ...
instrAsm (IOr a1 a2) = ...- The actual
compilePrim2function
Do in class
Exercise: Comparisons via Bit-Twiddling
- Can compute
arg1 > arg2by computingarg2 < arg1. - Can compute
arg1 != arg2by computingarg1 < arg2 || arg2 < arg1 - Can compute
arg1 = arg2by computing! (arg1 != arg2)
For the above, can you figure out how to implement:
- Boolean
!? - Boolean
||? - Boolean
&&?
You may find these instructions useful
4. Dynamic Checking
We’ve added support for Number and Boolean but we have no way to ensure that we don’t write gibberish programs like:
2 + trueor
7 < falseIn fact, lets try to see what happens with our code on the above:
ghci> exec "2 + true"Oops.
Static vs. Dynamic Type Checking
Later we will add a static type system
- that rejects meaningless programs at compile time.
Now lets add a dynamic system
- that aborts execution with wrong operands at run time.
Checking Tags at Run-Time
Here are the allowed types of operands for each primitive operation.
| Operation | Op-1 | Op-2 |
|---|---|---|
+ |
int |
int |
- |
int |
int |
* |
int |
int |
< |
int |
int |
> |
int |
int |
&& |
bool |
bool |
|| |
bool |
bool |
! |
bool |
|
if |
bool |
|
= |
int or bool |
int or bool |
Strategy: Asserting a Type
To check if arg is a number
Suffices to check that the LSB is
0If not, jump to special
error_non_intlabel
For example
mov rax, arg
mov rbx, rax ; copy into rbx register
and rbx, 0x00000001 ; extract lsb
cmp rbx, 0 ; check if lsb equals 0
jne error_non_number
...at error_non_number we can call into a C function:
error_non_number:
mov rdi, 0 ; pass error code
mov rsi, rax ; pass erroneous value
call error ; call run-time "error" functionFinally, the error function is part of the run-time and looks like:
void error(long code, long v){
if (code == 0) {
fprintf(stderr, "Error: expected a number but got %#010x\n", v);
}
else if (code == 1) {
// print out message for errorcode 1 ...
}
else if (code == 2) {
// print out message for errorcode 2 ...
} ...
exit(1);
}
Strategy By Example
Lets implement the above in a simple file tests/output/int-check.s
section .text
extern error
extern print
global our_code_starts_here
our_code_starts_here:
mov rax, 1 ; not a valid number
mov rbx, rax ; copy into rbx register
and rbx, 0x00000001 ; extract lsb
cmp rbx, 0 ; check if lsb equals 0
jne error_non_number
error_non_number:
mov rdi, 0
mov rsi, rax
call errorAlas
make tests/output/int-check.result
... segmentation fault ...What happened ?
Managing the Call Stack
To properly call into C functions (like error), we must play by the rules of the C calling convention
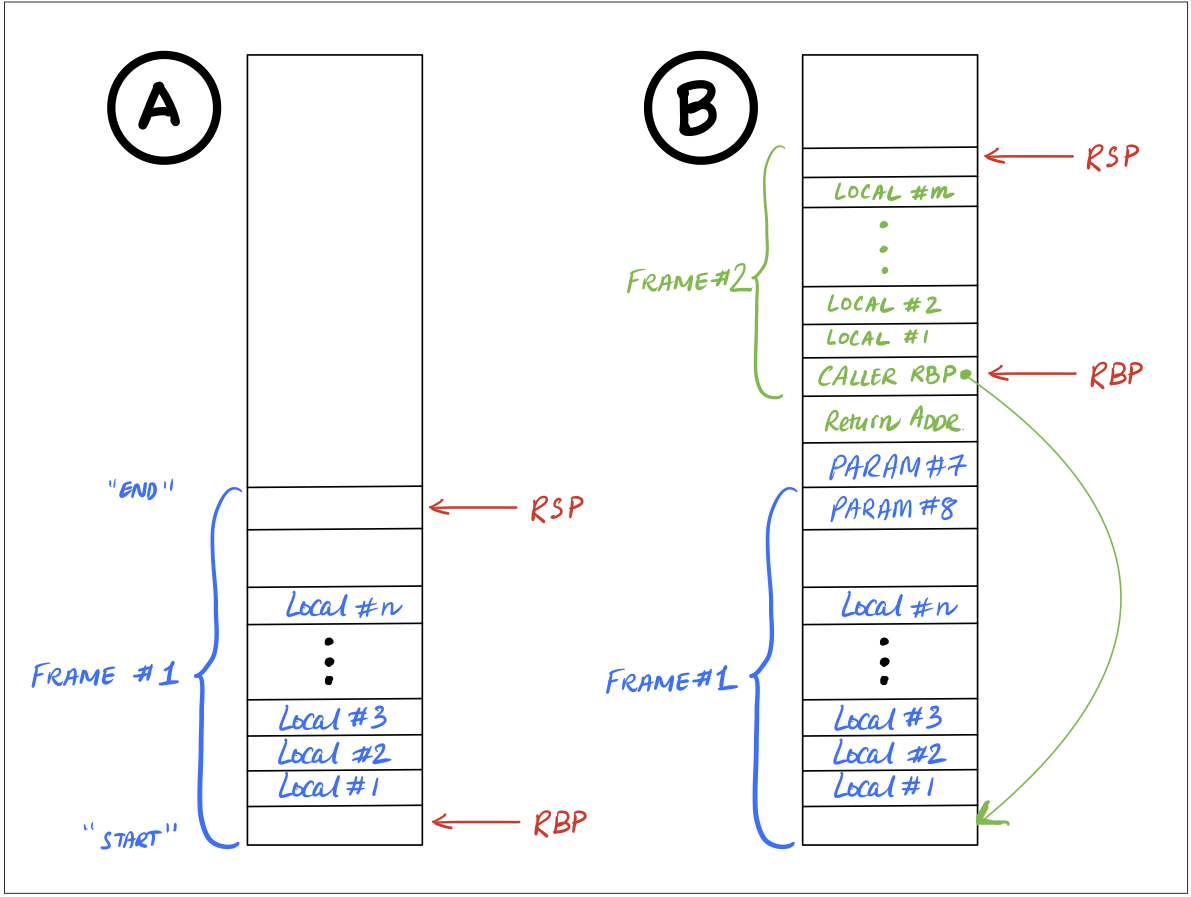
- The local variables of an (executing) function are saved in its stack frame.
- The start of the stack frame is saved in register
rbp, - The start of the next frame is saved in register
rsp.
Calling Convention
We must preserve the above invariant as follows:
In the Callee
At the start of the function
push rbp ; SAVE (previous) caller's base-pointer on stack
mov rbp, rsp ; set our base-pointer using the current stack-pointer
sub rsp, 8*N ; ALLOCATE space for N local variablesAt the end of the function
add rsp, 8*N0 ; FREE space for N local variables
pop rbp ; RESTORE caller's base-pointer from stack
ret ; return to caller
Fixed Strategy By Example
Lets implement the above in a simple file tests/output/int-check.s
section .text
extern error
extern print
global our_code_starts_here
our_code_starts_here:
push rbp ; save caller's base-pointer
mov rbp, rsp ; set our base-pointer
sub rsp, 1600 ; alloc '100' vars
mov rax, 1 ; not a valid number
mov rbx, rax ; copy into rbx register
and rbx, 0x00000001 ; extract lsb
cmp rbx, 0 ; check if lsb equals 0
jne error_non_number
add rsp, 1600 ; de-alloc '100' vars
pop rbp ; restore caller's base-pointer
ret
error_non_number:
mov rdi, 0
mov rsi, rax
call errorAha, now the above works!
make tests/output/int-check.result
... expected number but got ...Q: What NEW thing does our compiler need to compute?
Hint: Why do we sub esp, 1600 above?
Types
Lets implement the above strategy.
To do so, we need a new data type for run-time types:
data Ty = TNumber | TBooleana new Label for the error
data Label
= ...
| TypeError Ty -- Type Error Labels
| Builtin Text -- Functions implemented in Cand thats it.
Transforms
The compiler must generate code to:
- Perform dynamic type checks,
- Exit by calling
errorif a failure occurs, - Manage the stack per the convention above.
1. Type Assertions
The key step in the implementation is to write a function
assertType :: Env -> IExp -> Ty -> [Instruction]
assertType env v ty
= [ IMov (Reg RAX) (immArg env v)
, IMov (Reg RBX) (Reg RAX)
, IAnd (Reg RBX) (HexConst 0x00000001)
, ICmp (Reg RBX) (typeTag ty)
, IJne (TypeError ty)
]where typeTag is:
typeTag :: Ty -> Arg
typeTag TNumber = HexConst 0x00000000
typeTag TBoolean = HexConst 0x00000001 You can now splice assertType prior to doing the actual computations, e.g.
compilePrim2 :: Env -> Prim2 -> ImmE -> ImmE -> [Instruction]
compilePrim2 env Plus v1 v2 = assertType env v1 TNumber
++ assertType env v2 TNumber
++ [ IMov (Reg RAX) (immArg env v1)
, IAdd (Reg RAX) (immArg env v2)
]2. Errors
We must also add code at the TypeError TNumber and TypeError TBoolean labels.
errorHandler :: Ty -> Asm
errorHandler t =
[ ILabel (TypeError t) -- the expected-number error
, IMov (Reg RDI) (ecode t) -- set the first "code" param,
, IMov (Reg RSI) (Reg RAX) -- set the second "value" param first,
, ICall (Builtin "error") -- call the run-time's "error" function.
]
ecode :: Ty -> Arg
ecode TNumber = Const 0
ecode TBoolean = Const 1
3. Stack Management
Maintaining rsp and rbp
We need to make sure that all our code respects the C calling convention..
To do so, just wrap the generated code, with instructions to save and restore rbp and rsp
compileBody :: AnfTagE -> Asm
compileBody e = entryCode e
++ compileEnv emptyEnv e
++ exitCode e
entryCode :: AnfTagE -> Asm
entryCode e = [ IPush (Reg RBP) -- SAVE caller's RBP
, IMov (Reg RBP) (Reg RSP) -- SET our RBP
, ISub (Reg RSP) (Const (argBytes n)) -- ALLOC n local-vars
]
where
n = countVars e
exitCode :: AnfTagE -> Asm
exitCode e = [ IAdd (Reg RSP) (Const (argBytes n)) -- FREE n local-vars
, IPop (Reg RBP) -- RESTORE caller's RBP
, IRet -- RETURN to caller
]
where
n = countVars ethe rsp needs to be a multiple of 16 so:
argBytes :: Int -> Int
argBytes n = 8 * n'
where
n' = if even n then n else n + 1Q: But how shall we compute countVars?
Here’s a shady kludge:
countVars :: AnfTagE -> Int
countVars = 100Obviously a sleazy hack (why?), but lets use it to test everything else; then we can fix it.
4. Computing the Size of the Stack
Ok, now that everything (else) seems to work, lets work out:
countVars :: AnfTagE -> IntFinding the exact answer is undecidable in general (CSE 105), i.e. is impossible to compute.
However, it is easy to find an overapproximate heuristic, i.e.
a value guaranteed to be larger than the than the max size,
and which is reasonable in practice.
As usual, lets see if we can work out a heuristic by example.
QUIZ
How many stack slots/vars are needed for the following program?
1 + 2A. 0
B. 1
C. 2
QUIZ
How many stack slots/vars are needed for the following program?
let x = 1
, y = 2
, z = 3
in
x + y + zA. 0
B. 1
C. 2
D. 3
E. 4
QUIZ
How many stack slots/vars are needed for the following program?
if true:
let x = 1
, y = 2
, z = 3
in
x + y + z
else:
0A. 0
B. 1
C. 2
D. 3
E. 4
QUIZ
How many stack slots/vars are needed for the following program?
let x =
let y =
let z = 3
in z + 1
in y + 1
in x + 1A. 0
B. 1
C. 2
D. 3
E. 4
Strategy
Let countVars e be:
The maximum number of let-binds in scope at any point inside
e, i.e.The maximum size of the
Envwhen compilinge
Lets work it out on a case-by-case basis:
- Immediate values like
NumberorVar- are compiled without pushing anything onto the
Env - i.e.
countVars= 0
- are compiled without pushing anything onto the
- Binary Operations like
Prim2 o v1 v2take immediate values,- are compiled without pushing anything onto the
Env - i.e.
countVars= 0
- are compiled without pushing anything onto the
- Branches like
If v e1 e2can go either way- can’t tell at compile-time
- i.e. worst-case is larger of
countVars e1andcountVars e2
- Let-bindings like
Let x e1 e2require- evaluating
e1and - pushing the result onto the stack and then evaluating
e2 - i.e. larger of
countVars e1and1 + countVars e2
- evaluating
Implementation
We can implement the above a simple recursive function:
countVars :: AnfTagE -> Int
countVars (If v e1 e2) = max (countVars e1) (countVars e2)
countVars (Let x e1 e2) = max (countVars e1) (1 + countVars e2)
countVars _ = 0
Naive Heuristic is Naive
The above method is quite simplistic. For example, consider the expression:
let x = 1
, y = 2
, z = 3
in
0countVars would tell us that we need to allocate 3 stack spaces but clearly none of the variables are actually used.
Will revisit this problem later, when looking at optimizations.
Recap
We just saw how to add support for
- Multiple datatypes (
numberandboolean) - Calling external functions
and in doing so, learned about
- Tagged Representations
- Calling Conventions
To get some practice, in your assignment, you will add:
- Dynamic Checks for Arithmetic Overflows (see the
joandjnooperations) - A Primitive
printoperation implemented by a function in thecrun-time.
And next, we’ll see how to add user-defined functions.
